All possible values of

Question:

All possible values of $\theta \in[0,2 \pi]$ for which $\sin 2 \theta+\tan 2 \theta>0$ lie in:

  1. (1) $\left(0, \frac{\pi}{2}\right) \cup\left(\pi, \frac{3 \pi}{2}\right)$

  2. (2) $\left(0, \frac{\pi}{4}\right) \cup\left(\frac{\pi}{2}, \frac{3 \pi}{4}\right) \cup\left(\pi, \frac{5 \pi}{4}\right) \cup\left(\frac{3 \pi}{2}, \frac{7 \pi}{4}\right)$

  3. (3) $\left(0, \frac{\pi}{2}\right) \cup\left(\frac{\pi}{2}, \frac{3 \pi}{4}\right) \cup\left(\pi, \frac{7 \pi}{6}\right)$

  4. (4) $\left(0, \frac{\pi}{4}\right) \cup\left(\frac{\pi}{2}, \frac{3 \pi}{4}\right) \cup\left(\frac{3 \pi}{2}, \frac{11 \pi}{6}\right)$

Correct Option: , 2

Solution:

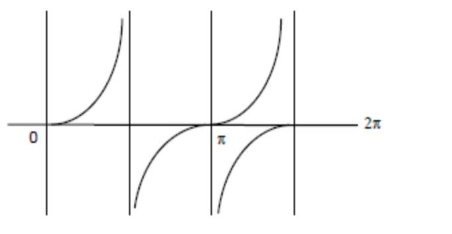
$\tan 2 \theta(1+\cos 2 \theta)>0$

$2 \theta \in\left(0, \frac{\pi}{2}\right) \cup\left(\pi, \frac{3 \pi}{2}\right) \cup\left(2 \pi, \frac{5 \pi}{2}\right) \cup\left(3 \pi, \frac{7 \pi}{2}\right)$

$\Rightarrow \theta \in\left(0, \frac{\pi}{4}\right) \cup\left(\frac{\pi}{2}, \frac{3 \pi}{4}\right) \cup\left(\pi, \frac{5 \pi}{4}\right) \cup\left(\frac{3 \pi}{2}, \frac{7 \pi}{4}\right)$

Leave a comment

eSaral Gurukul

NEET

JEE Main

JEE Advanced

Our Telegram Channel

All Study Material