An aeroplane left 50 minutes later than its scheduled time,

Let the usual speed of aero plane be $x \mathrm{~km} / \mathrm{hr}$. Then,

Increased speed of the aero plane $=(x+250) \mathrm{km} / \mathrm{hr}$

Time taken by the aero plane under usual speed to cover $1250 \mathrm{~km}=\frac{1250}{x} \mathrm{hr}$

Time taken by the aero plane under increased speed to cover $1250 \mathrm{~km}=\frac{1250}{(x+250)} \mathrm{hr}$

Therefore,

$\frac{1250}{x}-\frac{1250}{(x+250)}=\frac{50}{60}$

$\frac{\{1250(x+250)-1250 x\}}{x(x+250)}=\frac{5}{6}$

$\frac{1250 x+312500-1250 x}{x^{2}+250 x}=\frac{5}{6}$

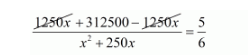
$1875000=5 x^{2}+1250 x$

$5 x^{2}+1250 x-1875000=0$

$5\left(x^{2}+250 x-375000\right)=0$

$x^{2}+250 x-375000=0$

$x^{2}-500 x+750 x-375000=0$

$x(x-500)+750(x-500)=0$

$(x-500)(x+750)=0$

So, either 

$(x-500)=0$

$x=500$

Or

$(x+750)=0$

$x=-750$

But, the speed of the aero plane can never be negative.

Hence, the usual speed of train is $x=500 \mathrm{~km} / \mathrm{hr}$