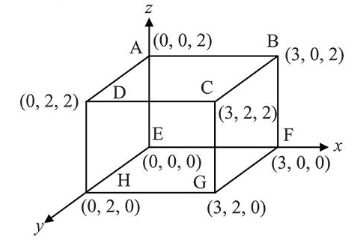
An electric field $\overrightarrow{\mathrm{E}}=4 x \hat{i}-\left(y^{2}+1\right) \hat{j} \mathrm{~N} / \mathrm{C}$ passes through the box shown in figure. The flux of the electric field through surfaces $\mathrm{ABCD}$ and BCGF are marked as $\phi_{1}$ and $\phi_{11}$ respectively. The difference between $\left(\phi_{1}-\phi_{11}\right)$ is (in $\mathrm{Nm}^{2} / \mathrm{C}$ )_________
$(-48)$
Flux of electric field $\vec{E}$ through any area $\vec{A}$ is defined as
$\phi=\int E \cdot A \cos \theta$
Here, $\theta=$ angle between electric field and area vector of a surface
For surface $A B C D$ Angle, $\theta=90^{\circ}$
$\therefore \quad \phi_{1}=\int E \cdot A \cos 90^{\circ}=0$
For surface $B C G F \phi_{n}=\int \vec{E} \cdot \overrightarrow{d A}$
$\therefore \phi_{11}=\left[4 \times \hat{i}-\left(y^{2}+1\right) \hat{j}\right] \cdot 4 \hat{i}=16 x$
$\phi_{11}=48 \frac{\mathrm{Nm}^{2}}{C}$
$\phi_{1}-\phi_{11}=-48$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.