Question:
An electron with kinetic energy $K_{1}$ enters between parallel plates of a capacitor at an angle ' $\alpha$ ' with the plates. It leaves the plates at angle ' $\beta$ ' with kinetic energy $K_{2}$. Then the ratio of kinetic energies $K_{1}: K_{2}$ will be :
Correct Option: , 2
Solution:
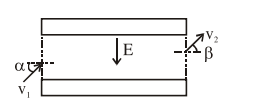
velocity along the plate will not change.
$\therefore v_{1} \cos \alpha=v_{2} \cos \beta$
$\frac{K_{1}}{K_{2}} \Rightarrow \frac{v_{1}^{2}}{v_{2}^{2}}=\frac{\cos ^{2} \beta}{\cos ^{2} \alpha}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
