An engine of a train, moving with uniform acceleration, passes the signal post with velocity $u$ and the last compartment with velocity v. The velocity with which middle point of the train passes the signal post is :
Correct Option: , 3
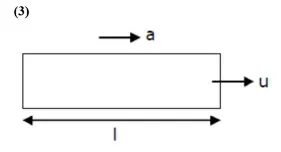
$\mathrm{a}=$ uniform acceleration
$\mathbf{u}=$ velocity of first compartment $\mathrm{v}=$ velocity of last compartment $\mid=$ length of train
$v^{2}=u^{2}+2$ as $\left(3^{\text {rd }}\right.$ equation of motion $) \mathrm{v}^{2}=\mathrm{u}^{2}+2 \mathrm{al}$
$\mathrm{v}_{\text {middle }}^{2}=\mathrm{u}^{2}+2 \mathrm{a} \frac{1}{2}$
$\therefore \mathrm{v}_{\text {middle }}^{2}=\mathrm{u}^{2}+\mathrm{al} \quad \ldots(2)$
from equation (1) and (2) $\mathrm{v}_{\text {middle }}^{2}=\mathrm{u}^{2}+\left(\frac{\mathrm{v}^{2}-\mathrm{u}^{2}}{2}\right)$
$=\frac{u^{2}+u^{2}}{2}$
$\therefore \mathrm{v}_{\text {middle }}=\sqrt{\frac{\mathrm{v}^{2}+\mathrm{u}^{2}}{2}}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.