An express train takes 1 hour less than a passenger train to travel 132 km

Let the speed of the passenger train be $x \mathrm{~km} / \mathrm{hr}$. Then,

Speed of the express train $=(x+11) \mathrm{km} / \mathrm{hr}$

Time taken by the passenger train to cover $132 \mathrm{~km}$ between Mysore to Bangalore $=\frac{132}{x} \mathrm{hr}$

Time taken by the express train to cover $132 \mathrm{~km}$ between Mysore to Bangalore $=\frac{132}{(x+11)}$ hr

Therefore,

$\frac{132}{x}-\frac{132}{(x+11)}=1$

$\frac{\{132(x+11)-132 x\}}{x(x+11)}=1$

$\frac{132 x+1452-132 x}{x^{2}+11 x}=1$

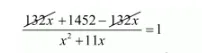
$1452=x^{2}+11 x$

$x^{2}+11 x-1452=0$

$x^{2}+11 x-1452=0$

$x^{2}-33 x+44 x-1452=0$

$x(x-33)+44(x-33)=0$

$(x-33)(x+44)=0$

So, either 

$(x-33)=0$

$x=33$

Or

$(x+44)=0$

$x=-44$

Eut, the speed of the train can never be negative.

Thus, when $x=33$ then speed of express train

$=(x+11)$

$=(33+11)$

$=44$

Hence, the speed of the passenger train is $x=33 \mathrm{~km} / \mathrm{hr}$

and the speed of the express train is $x=44 \mathrm{~km} / \mathrm{hr}$ respectively.