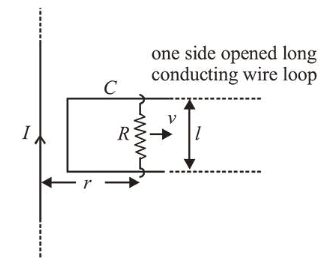
An infinitely long straight wire carrying current $I$, one side opened rectangular loop and a conductor $C$ with a sliding connector are located in the same plane, as shown in the figure. The connector has length $l$ and resistance $R$. It slides to the right with a velocity $v$. The resistance of the conductor and the self inductance of the loop are negligible. The induced current in the loop, as a function of separation $r$, between the connector and the straight wire is :
Correct Option: 4,
(4) Magnetic field at a distance $r$ from the wire
$B=\frac{\mu_{0} I}{2 \pi r}$
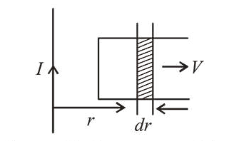
Magnetic flux for small displacement $d r$;
\phi=B \cdot A=B l d r \quad\left[\because A=l d r\right.$ and $\left.B \cdot A=B A \cos 0^{\circ}\right]$
$\Rightarrow \phi=\frac{\mu_{0} I}{2 \pi r} l d r$
Emf, $e=\frac{d \phi}{d t}=\frac{\mu_{0} I l}{2 \pi r} \cdot \frac{d r}{d t} \Rightarrow e=\frac{\mu_{0}}{2 \pi} \cdot \frac{I v l}{r}$
Induce current in the loop, $i=\frac{e}{R}=\frac{\mu_{0}}{2 \pi} \cdot \frac{I v l}{R r}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.