Question:
An insect is at the bottom of a hemispherical ditch of radius $1 \mathrm{~m}$. It crawls up the ditch but starts slipping after it is at height $h$ from the bottom. If the coefficient of friction between the ground and the insect is $0.75$, then $h$ is : $\left(\mathrm{g}=10 \mathrm{~ms}^{-2}\right)$
Correct Option: 1
Solution:
(1) For balancing, $m g \sin \theta=f=\mu m g \cos \theta$
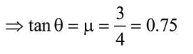
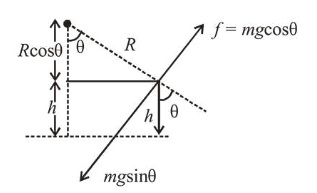
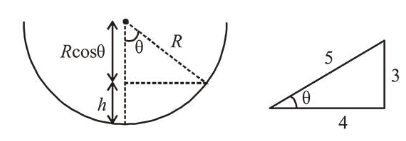
$h=R-R \cos \theta=R-R\left(\frac{4}{5}\right)=\frac{R}{5}$
$\therefore h=\frac{R}{5}=0.2 \mathrm{~m}$ $[\because$ radius, $R=1 \mathrm{~m}]$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.