An observer, 1.5 m tall, is 28.5 m away from a a tower 30 m high

Let $B E$ be the observer of $1.5 \mathrm{~m}$ tall. And $A D$ be the tower of height 30 . Here we have to find angle of elevation of the top of tower.

Let $\angle A B C=\theta$

The corresponding figure is as follows

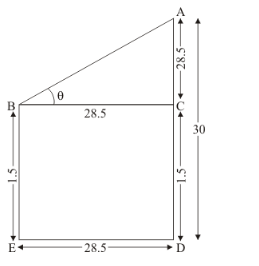
$\ln \triangle A B C$,

$\Rightarrow \quad \tan \theta=\frac{A C}{B C}$

$\Rightarrow \quad \tan \theta=\frac{28.5}{28.5}$

$\Rightarrow \quad \tan \theta=1$

$\Rightarrow \quad \theta=45^{\circ}$

Hence the required angle is $45^{\circ}$.