An organisation selected 2400 families at random and surveyed them to determine a relationship between the income level and the number of vehicles in a family.
An organisation selected 2400 families at random and surveyed them to determine a relationship between the income level and the number of vehicles in a family. The information gathered is listed in the table below:
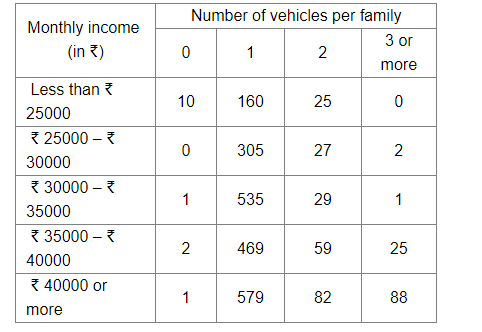
Suppose a family is chosen at random. Find the probability that the family chosen is
(i) earning ₹ 25000 – ₹ 30000 per month and owning exactly 2 vehicles.
(ii) earning ₹ 40000 or more per month and owning exactly 1 vehicle.
(iii) earning less than ₹ 25000 per month and not owning any vehicle.
(iv) earning ₹ 35000 – ₹ 40000 per month and owning 2 or more vehicles.
(v) owning not more than 1 vehicle.
Number of families surveyed = 2400
(i) Number of families earning ₹ 25000 – ₹ 30000 per month and owning exactly 2 vehicles = 27
∴ P(Family chosen is earning ₹ 25000 – ₹ 30000 per month and owning exactly 2 vehicles)
= Number of families earning ₹ 25000 – ₹ 30000 per month and owning exactly 2 vehicles / Number of families surveyed
$=\frac{27}{2400}$
$=\frac{9}{800}$
(ii) Number of families earning ₹ 40000 or more per month and owning exactly 1 vehicle = 579
∴ P(Family chosen is earning ₹ 40000 or more per month and owning exactly 1 vehicle)
= Number of families earning ₹ 40000 or more per month and owning exactly 1 vehicle / Number of families surveyed
$=\frac{579}{2400}$
$=\frac{193}{800}$
(iii) Number of families earning less than ₹ 25000 per month and not owning any vehicle = 10
∴ P(Family chosen is earning less than ₹ 25000 per month and not owning any vehicle)
= Number of families earning less than ₹ 25000 per month and not owning any vehicle / Number of families surveyed
$=\frac{10}{2400}$
$=\frac{1}{240}$
(iv) Number of families earning ₹ 35000 – ₹ 40000 per month and owning 2 or more vehicles = 59 + 25 = 84
∴ P(Family chosen is earning ₹ 35000 – ₹ 40000 per month and owning 2 or more vehicles)
= Number of families earning ₹ 35000 – ₹ 40000 per month and owning 2 or more vehicles / Number of families surveyed
$=\frac{84}{2400}$
$=\frac{7}{200}$
(v) Number of families owning not more than 1 vehicle
= Number of families owning 0 vehicle + Number of families owning 1 vehicle
= 10 + 0 + 1 + 2 + 1 + 160 + 305 + 535 + 469 + 579 = 2062
∴ P(Family chosen is owning not more than 1 vehicle)
= Number of families owning not more than 1 vehicle / Number of families surveyed
$=\frac{2062}{2400}$
$=\frac{1031}{1200}$
