AP and PQ are tangents drawn from a point A to a circle with

Solution:

Let us first put the given data in the form of a diagram.

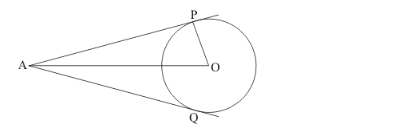
We know that the radius of the circle will always be perpendicular to the tangent at the point of contact. Therefore,

$O P \perp A P$

$A P^{2}=O A^{2}-O P^{2}$

$A P^{2}=15^{2}-9^{2}$

$A P^{2}=225-81$

 

$A P^{2}=144$

$A P=\sqrt{144}$

 

$A P=12$

Since tangents drawn from an external point will be equal in length,

AP = AQ

Since, AP = 12

AQ = 12

AP + AQ = 12 + 12

AP + AQ = 24

Therefore option (c) is the correct answer to this question.