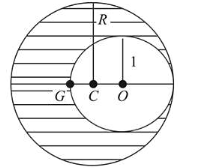
As shown in fig. when a spherical cavity (centred at $O$ ) of radius 1 is cut out of a uniform sphere of radius $R$ (centred at $C$ ), the centre of mass of remaining (shaded) part of
sphere is at $G$, i.e on the surface of the cavity. $R$ can be determined by the equation:
Correct Option:
(1) Mass of sphere = volume of sphere $x$ density of sphere
$=\frac{4}{3} \pi R^{3} \rho$
Mass of cavity $M_{\text {cavity }}=\frac{4}{3} \pi(1)^{3} \rho$
Mass of remaining $M_{\text {(Remaining) }}=\frac{4}{3} \pi R^{3} \rho-\frac{4}{3} \pi(1)^{3} \rho$
Centre of mass of remaining part,
$X_{\mathrm{COM}}=\frac{M_{1} r_{1}+M_{2} r_{2}}{M_{1}+M_{2}}$
$\Rightarrow-(2-R)=\frac{\left[\frac{4}{3} \pi R^{3} \rho\right] 0+\left[\frac{4}{3} \pi(1)^{3}(-\rho)\right][R-1]}{\frac{4}{3} \pi R^{3} \rho+\frac{4}{3} \pi(1)^{3}(-\rho)}$
$\Rightarrow \frac{(R-1)}{\left(R^{3}-1\right)}=2-R$
$\Rightarrow \frac{(R-1)}{(R-1)\left(R^{2}+R+1\right)}=2-R$
$\Rightarrow\left(R^{2}+R+1\right)(2-R)=1$
