Assertion (A) If two tangents are drawn to a circle from an external point,

(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not a correct explanation of Assertion (A).

Assertion :-
We know that if two tangents are drawn to a circle from an external point, they subtend equal angles at the centre.

Reason:-

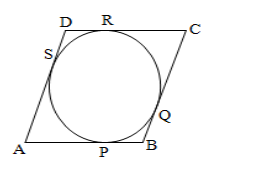
Given, a parallelogram ABCD circumscribes a circle with centre O.

$A B=B C=C D=A D$

We know that the tangents drawn from an external point to circle are equal .

$\therefore A P=A S \ldots \ldots \ldots(i) \quad[$ tangents from $A]$

$B P=B Q \ldots \ldots \ldots .(i i) \quad[$ tangents from $B]$

$C R=C Q \ldots \ldots \ldots$ (iii) $\quad[$ tangents from $C]$

$D R=D S \ldots \ldots \ldots \ldots(i v) \quad[$ tangents from $D]$

$\therefore A B+C D=A P+B P+C R+D R$

$=A S+B Q+C Q+D S[$ from $(i),(i i),(i i i)$ and $(i v)]$

$=(A S+D S)+(B Q+C Q)$

$=A D+B C$

Thus, $(A B+C D)=(A D+B C)$

$\Rightarrow 2 A B=2 A D[\because$ opposite sides of a parallelogram are equal $]$

$\Rightarrow A B=A D$

$\therefore C D=A B=A D=B C$

Hence, ABCD is a rhombus.