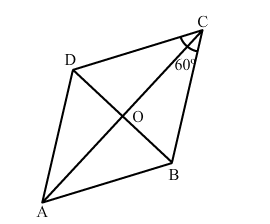
Assertion: If ABCD is a rhombus whose one angle is 60°,

Solution:

(b) Both Assertion and Reason are true but Reason is not a correct explanation of Assertion.

Reason (R) is clearly true.
The explanation of assertion (A)​ is as follows:
ABCD is a rhombus. So, all of its sides are equal.
Now, BC = DC

$\Rightarrow \angle B D C=\angle D B C=x^{\circ}$

Also, $\angle B C D=60^{\circ}$

$\therefore x^{\circ}+x^{\circ}+60^{\circ}=180^{\circ}$

$\Rightarrow 2 x^{\circ}=120^{\circ}$

$\Rightarrow x^{\circ}=60^{\circ}$

$\therefore \angle B C D=\angle B D C=\angle D B C=60^{\circ}$

So, ​∆BCD is an equilateral triangle.

i.e., BD = BC = a

$\therefore O B=\frac{a}{2}$

Now, in $\triangle \mathrm{OAB}$, we have:

$O A^{2}=A B^{2}-O B^{2}=a^{2}-\left(\frac{a}{2}\right)^{2}=\frac{3 a^{2}}{4}$

$\Rightarrow O A=\frac{\sqrt{3} a}{2}$

$\therefore A C: B D=\sqrt{3} a: a=\sqrt{3}: 1$

Thus, assertion (A)​ is also true, but reason (R) does not give (A).
​Hence, the correct answer is (b).