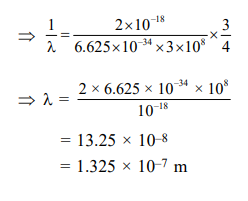Question:
Based on the equation
$\Delta \mathrm{E}=-2.0 \times 10^{-18} \mathrm{~J}\left(\frac{1}{\mathrm{n}_{2}^{2}}-\frac{1}{\mathrm{n}_{1}^{2}}\right)$
the wavelength of the light that must be absorbed to excite hydrogen electron from level $\mathrm{n}=$ 1 to level $\mathrm{n}=2$ will be $\left(\mathrm{h}=6.625 \times 10^{-34} \mathrm{Js}, \mathrm{C}=3 \times 10^{8} \mathrm{~ms}^{-1}\right)$
Correct Option: , 2
Solution:
$\frac{1}{\lambda}=\frac{2 \times 10^{-18}}{\mathrm{hc}}\left[\frac{1}{(1)^{2}}-\frac{1}{(2)^{2}}\right]$