Blocks of masses m, 2 m, 4 m and 8 m are arranged in a line on a frictionless floor.

(2) According to the question, all collisions are perfectly inelastic, so after the final collision, all blocks are moving together.

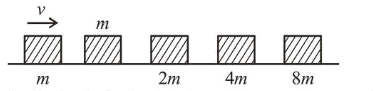
Let the final velocity be $v^{\prime}$, using momentum conservation

$m v=16 m v^{\prime} \Rightarrow v^{\prime}=\frac{v}{16}$

Now initial energy $E_{i}=\frac{1}{2} m v^{2}$

Final energy: $E_{f}=\frac{1}{2} \times 16 m \times\left(\frac{v}{16}\right)^{2}=\frac{1}{2} \frac{m v^{2}}{16}$

Energy loss : $E_{i}-E_{f}=\frac{1}{2} m v^{2}-\frac{1}{2} m \frac{v^{2}}{16}$

$\Rightarrow \frac{1}{2} m v^{2}\left[1-\frac{1}{16}\right] \Rightarrow \frac{1}{2} m v^{2}\left[\frac{15}{16}\right]$

The total energy loss is $P \%$ of the original energy.

$\therefore \% P=\frac{\text { Energy loss }}{\text { Original energy }} \times 100$

$=\frac{\frac{1}{2} m v^{2}\left[\frac{15}{16}\right]}{\frac{1}{2} m v^{2}} \times 100=93.75 \%$

Hence, value of $P$ is close to 94 .