Consider a $20 \mathrm{~kg}$ uniform circular disk of radius $0.2 \mathrm{~m}$. It is pin supported at its center and is at rest initially. The disk is acted upon by a constant force $\mathrm{F}=20 \mathrm{~N}$ through a massless string wrapped around its periphery as shown in the figure.
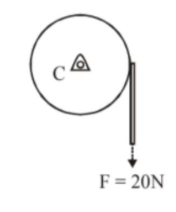
Suppose the disk makes $\mathrm{n}$ number of revolutions to attain an angular speed of $50 \mathrm{rads}^{-1}$. The value of $\mathrm{n}$, to the nearest integer, is_____ [Given : In one complete revolution, the disk rotates by $6.28 \mathrm{rad}$ ]
(20)
$\alpha=\frac{\tau}{\mathrm{I}}=\frac{\mathrm{F} \cdot \mathrm{R}}{\mathrm{mR}^{2} / 2}=\frac{2 \mathrm{~F}}{\mathrm{mR}}$
$\alpha=\frac{2 \times 200}{20 \times(0.2)}=10 \mathrm{rad} / \mathrm{s}^{2}$
$\omega^{2}=\omega_{0}^{2}+2 \alpha \Delta \theta$
$(50)^{2}=0^{2}+2(10) \Delta \theta \Rightarrow \Delta \theta=\frac{2500}{20}$\
$\Delta \theta=125 \mathrm{rad}$
No. of $=\frac{125}{2 \pi} \approx 20$ revolution
