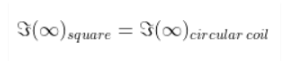Question:
Consider a circular current-carrying loop of radius R in the x-y plane with centre at the origin. Consider the line integral
$\Im(L)=\left|\int_{-L}^{L} B \cdot d l\right|$ taken along z-axis.
(a) show that
$\Im(L)$ monotonically increases with $\mathrm{L}$
(b) use an appropriate Amperian loop to that

(c) verify directly the above result
(d) suppose we replace the circular coil by a square coil of sides R carrying the same current I. What can you say about
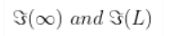
Solution:
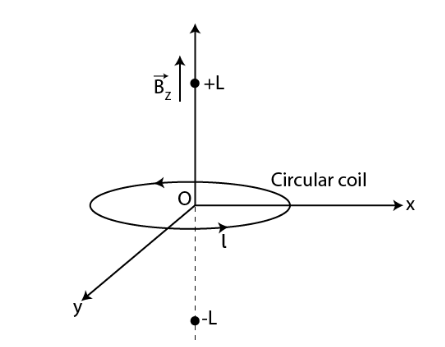
(a) Magnetic field due to a circular current-carrying loop is given as
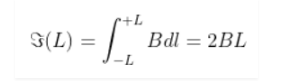
It is a monotonically increasing function of L
(b) The Amperian loop is given as
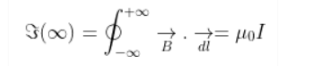
(c) The magnetic field at the axis of the circular coil is given as μ0I
(d) When a circular coil is replaced with a square coil, it is given as