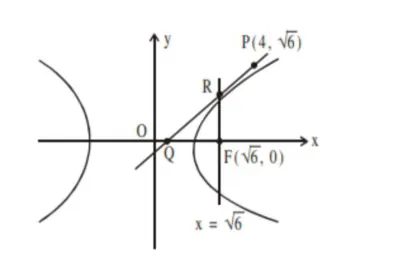
Consider a hyperbola $\mathrm{H}: \mathrm{x}^{2}-2 \mathrm{y}^{2}=4$. Let the tangent at a point $\mathrm{P}(4, \sqrt{6})$ meet the $\mathrm{x}$-axis at $\mathrm{Q}$ and latus rectum at $\mathrm{R}\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right), \mathrm{x}_{1}>0$. If $\mathrm{F}$ is a focus of $\mathrm{H}$ which is nearer to the point $\mathrm{P}$, then the area of $\Delta Q F R$ is equal to
Correct Option: , 3
$\frac{x^{2}}{4}-\frac{y^{2}}{2}=1$
$\mathrm{e}=\sqrt{1+\frac{\mathrm{b}^{2}}{\mathrm{a}^{2}}}=\sqrt{\frac{3}{2}}$
Focus $\mathrm{F}(\mathrm{ae}, 0) \Rightarrow \mathrm{F}(\sqrt{6}, 0)$
equation of tangent at $\mathrm{P}$ to the hyperbola is
$2 x-y \sqrt{6}=2$
tangent meet $\mathrm{x}$-axis at $\mathrm{Q}(1,0)$
$\backslash$ \& latus rectum $x=\sqrt{6}$ at $R\left(\sqrt{6}, \frac{2}{\sqrt{6}}(\sqrt{6}-1)\right)$
$\therefore$ Area of $\Delta_{\mathrm{QFR}}=\frac{1}{2}(\sqrt{6}-1) \cdot \frac{2}{\sqrt{6}}(\sqrt{6}-1)$
$=\frac{7}{\sqrt{6}}-2$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.