Consider a region $R=\left\{(x, y) \in \mathbf{R}^{2}: x^{2} \leq y \leq 2 x\right\}$. If a line $y=\alpha$ divides the area of region $R$ into two equal parts, then which of the following is true?
Correct Option: , 2
Let $y=x^{2}$ and $y=2 x$
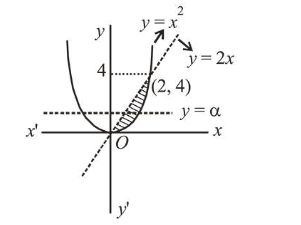
According to question
$\therefore \int_{0}^{\alpha}\left(\sqrt{y}-\frac{y}{2}\right) d y=\int_{\alpha}^{4}\left(\sqrt{y}-\frac{y}{2}\right) d y$
$\Rightarrow\left[\frac{y^{3 / 2}}{\frac{3}{2}}\right]_{0}^{\alpha}-\left[\frac{y^{2}}{4}\right]_{0}^{\alpha}=\left[\frac{y^{3 / 2}}{\frac{3}{2}}\right]_{\alpha}^{4}-\left[\frac{y^{2}}{4}\right]_{\alpha}^{4}$
$\Rightarrow \frac{2}{3} \alpha^{3 / 2}-\frac{\alpha^{2}}{4}=\frac{2}{3}\left(8-\alpha^{3 / 2}\right)-\frac{1}{4}\left(16-\alpha^{2}\right)$
$\Rightarrow \frac{4}{3} \alpha^{3 / 2}-\frac{\alpha^{2}}{2}=\frac{4}{3} \Rightarrow 8 \alpha^{3 / 2}-3 \alpha^{2}=8$
$\therefore 3 \alpha^{2}-8 \alpha^{3 / 2}+8=0$
