Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another

Given that

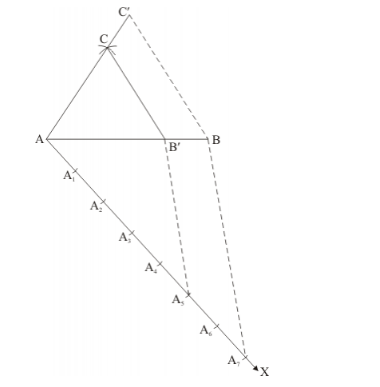
Construct a triangle of sides $A B=5 \mathrm{~cm}, B C=6 \mathrm{~cm}$ and $A C=7 \mathrm{~cm}$ and then a triangle similar to it whose sides are $(7 / 5)^{\text {th }}$ of the corresponding sides of $\triangle A B C$.

We follow the following steps to construct the given

Step of construction

Step: I- First of all we draw a line segment.

Step: II- With A as centre and radius, draw an arc.

Step: III- With B as centre and radius, draw an arc, intersecting the arc drawn in step II at C.

Step: IV- Joins AC and BC to obtain.

Step: V- Below AB, makes an acute angle.

Step: VI- Along $A X_{x}$ mark off seven points $A_{1}, A_{2}, A_{3}, \mathrm{~A}_{4}, \mathrm{~A}_{5}, A_{6}$ and $A_{7}$ such that $A A_{1}=A_{1} A_{2}=A_{2} A_{3}=A_{3} A_{4}=A_{4} A_{5}=A_{5} A_{6}=A_{6} A_{7}$

Step: VII-Join $A_{5} B$.

Step: VIII- Since we have to construct a triangle each of whose sides is $(7 / 5)^{\text {th }}$ of the corresponding sides of $\triangle A B C$.

So, we draw a line $A_{3} B^{\prime}$ on $A X$ from point $A_{7}$ which is $A_{7} B^{\prime} \| A_{5} B$, and meeting $A B$ at $B$ '.

Step: IX- From $B^{\prime}$ point draw $B^{\prime} C^{\prime} \| B C$, and meeting $A C$ at $C^{\prime}$

Thus, $\triangle A B C^{\prime}$ is the required triangle, each of whose sides is $(7 / 5)$ it of the corresponding sides of $\triangle A B C$.