Construct an equilateral triangle,

Solution:

Let us draw an equilateral triangle of side 5 cm. We know that all sides of an equilateral triangle are equal. Therefore, all sides of the equilateral triangle will be 5 cm. We also know that each angle of an equilateral triangle is 60º.

The below given steps will be followed to draw an equilateral triangle of 5 cm side.

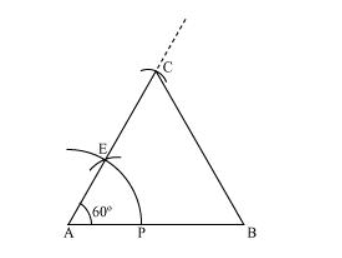
Step I: Draw a line segment AB of 5 cm length. Draw an arc of some radius, while taking A as its centre. Let it intersect AB at P.

Step II: Taking P as centre, draw an arc to intersect the previous arc at E. Join AE.

Step III: Taking A as centre, draw an arc of 5 cm radius, which intersects extended line segment AE at C. Join AC and BC. ΔABC is the required equilateral triangle of side 5 cm.



Justification of Construction:

We can justify the construction by showing $A B C$ as an equilateral triangle i.e., $A B=B C=A C=5 \mathrm{~cm}$ and $\angle A=\angle B=\angle C=60^{\circ}$.

In $\triangle A B C$, we have $A C=A B=5 \mathrm{~cm}$ and $\angle A=60^{\circ}$.

Since $A C=A B$

$\angle B=\angle C$ (Angles opposite to equal sides of a triangle)

In $\triangle \mathrm{ABC}$,

$\angle A+\angle B+\angle C=180^{\circ}$ (Angle sum property of a triangle)

$\Rightarrow 60^{\circ}+\angle C+\angle C=180^{\circ}$

$\Rightarrow 2 \angle C=180^{\circ}-60^{\circ}=120^{\circ}$

$\Rightarrow \angle C=60^{\circ}$

$\therefore \angle B=\angle C=60^{\circ}$

We have, $\angle A=\angle B=\angle C=60^{\circ} \ldots$ (1)

$\Rightarrow \angle A=\angle B$ and $\angle A=\angle C$

$B C=A C$ and $B C=A B$ (Sides opposite to equal angles of a triangle)

$\Rightarrow A B=B C=A C=5 \mathrm{~cm} \ldots(2)$

From equations (1) and (2), ΔABC is an equilateral triangle.