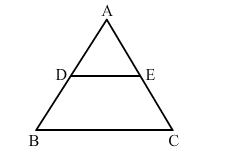
D and E are points on the sides AB and AC respectively of a

Solution:

(i) We have:

$\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{5.7}{9.5}=0.6 \mathrm{~cm}$

 

$\frac{\mathrm{AE}}{\mathrm{EC}}=\frac{4.8}{8}=0.6 \mathrm{~cm}$

Hence, $\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}$

Applying the converse of Thales' theorem,

we conclude that $\mathrm{DE} \| \mathrm{BC}$.

(ii)
We have:
AB = 11.7 cm, DB = 6.5 cm
Therefore,
AD = 11.7 -">−- 6.5 = 5.2 cm
Similarly,
AC = 11.2 cm, AE = 4.2 cm
Therefore,
EC = 11.2 -">−- 4.2 = 7 cm

Now,

$\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{5.2}{6.5}=\frac{4}{5}$

$\frac{\mathrm{AE}}{\mathrm{EC}}=\frac{4.2}{7}$

Thus, $\frac{\mathrm{AD}}{\mathrm{DB}} \neq \frac{\mathrm{AE}}{\mathrm{EC}}$

Applying the converse of Thales' theorem,
we conclude that DE is not parallel to BC.

(iii)
We have:
AB = 10.8 cm, AD = 6.3 cm
Therefore,
DB = 10.8 -">−- 6.3 = 4.5 cm
Similarly,
AC = 9.6 cm, EC = 4 cm
Therefore,
AE = 9.6 -">−- 4 = 5.6 cm
Now,

$\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{6.3}{4.5}=\frac{7}{5}$

$\frac{\mathrm{AE}}{\mathrm{EC}}=\frac{5.6}{4}=\frac{7}{5}$

$\Rightarrow \frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}$

Applying the converse of Thales' theorem,

we conclude that $\mathrm{DE} \| \mathrm{BC}$.

(iv)
We have:
AD = 7.2 cm, AB = 12 cm
Therefore,
DB = 12 -">−- 7.2 =  4.8 cm
Similarly,
AE = 6.4 cm, AC = 10 cm
Therefore,
EC = 10 -">−- 6.4 = 3.6 cm
Now,

$\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{7.2}{4.8}=\frac{3}{2}$

$\frac{\mathrm{AE}}{\mathrm{EC}}=\frac{6.4}{3.6}=\frac{16}{9}$

Thus, $\frac{\mathrm{AD}}{\mathrm{DB}} \neq \frac{\mathrm{AE}}{\mathrm{EC}}$

Applying the converse of Thales' theorem, we conclude that $\mathrm{DE}$ is not parallel to $\mathrm{BC}$.