Question:
D is any point on the side AC of ΔABC with AB = AC. Show that CD < BD.
Solution:
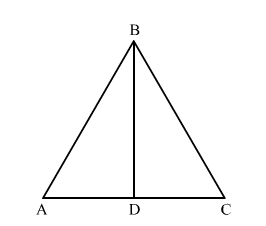
Given: In
To prove: CD < BD
Proof:
In
Since, AB = AC (Given)
So, $\angle A B C=\angle A C B$
In $\Delta A B C$ and $\Delta D B C$,
$\angle A B C>\angle D B C$
$\Rightarrow \angle A C B>\angle D B C \quad[$ From (i) $]$
$\Rightarrow B D>C D \quad$ (Side opposite to greater angle is longer.)
$\therefore C D
