Divide a line segment of length 9 cm internally in the ratio 4 : 3.

Solution:

Given that

Determine a point which divides a line segment of lengthinternally in the ratio of.

We follow the following steps to construct the given

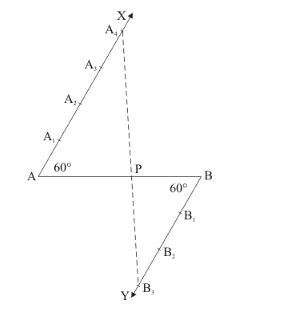
Step of construction

Step: I- First of all we draw a line segment.

Step: II- We draw a ray making an acute anglewith.

Step: III- Draw a ray parallel to AX by making an acute angle.

Step IV- Mark of two points on and three points on in such a way that.

Step: V- Joins  and this line intersects at a point P.

Thus, P is the point dividing  internally in the ratio of 

Justification:

In $\triangle A A_{4} P$ and $\triangle B B_{3} P$, we have

$\angle A_{4} A P=\angle P B B_{3}[\angle A B Y=\angle B A X]$

And $\angle A P A_{4}=\angle B P B_{3}[$ Vertically opposite angle $]$

So, AA similarity criterion, we have

$\triangle A A_{4} P \approx \Delta B B_{3} P$

$\frac{A A_{4}}{B B_{3}}=\frac{A P}{B P}$

$\frac{A P}{B P}=\frac{4}{3}$