Draw a circle of radius 4 cm.

In order to draw the pair of tangents, we follow the following steps
Steps of construction

1. Take a point 0 on the plane of the paper and draw a circle of radius OA = 4 cm.
2. Produce OA to B such that OA = AB = 4 cm.
3. Taking A as the centre draw a circle of radius AO = AB = 4 cm.
   Suppose it cuts the circle drawn in step 1 at P and Q.
4. Join BP and BQ to get desired tangents.

Justificatign in $\triangle O A P$, we have

$O A=O P=4 \mathrm{~cm}$ ( $\because$ Radius)

Also, $A P=4 \mathrm{~cm}$ ( $\because$ Radius of circle with centre $A$ )

$\therefore \Delta O A P$ is equilateral

$\Rightarrow \quad \angle P A O=60^{\circ}$

$\Rightarrow \quad \angle B A P=120^{\circ}$

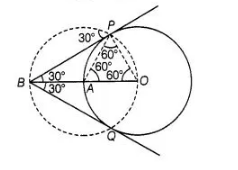
In $\triangle B A P$, we have

$B A=A P$ and $\angle B A P=120^{\circ}$

$\therefore \quad \angle A B P=\angle A P B=30^{\circ}$

$\Rightarrow \quad \angle P B Q=60^{\circ}$

Alternate Method

Steps of construction

1. Take a point $O$ on the plane of the paper and draw a circle with centre $O$ and radius

$O A=4 \mathrm{~cm}$.

2. At $O$ construct radii $O A$ and $O B$ such that to $\angle A O B$ equal $120^{\circ}$ i.e., supplement of the

angle between the tangents.

3. Draw perpendiculars to $O A$ and $O B$ at $A$ and $B$, respectively. Suppose these

perpendiculars intersect at $P$. Then, $P A$ and $P B$ are required tangents.

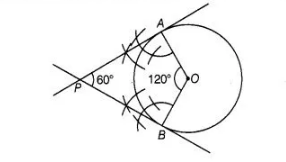
Justification

In quadrilateral $O A P B$, we have

$\angle O A P=\angle O B P=90^{\circ}

$and

$\angle A O B=120^{\circ}$

$\therefore \quad \angle O A P+\angle O B P+\angle A O B+\angle A P B=360^{\circ}$

$\Rightarrow \quad 90^{\circ}+90^{\circ}+120^{\circ}+\angle A P B=360^{\circ}$

$\therefore \quad \angle A P B=360^{\circ}-\left(90^{\circ}+90^{\circ}+120^{\circ}\right)$

$=360^{\circ}-300^{\circ}=60^{\circ}$