Draw a circle of radius 6 cm. From a point 10 cm away from its centre,

Given that

Construct a circle of radius, and form its centre, construct the pair of tangents to the circle.

Find the length of tangents.

We follow the following steps to construct the given

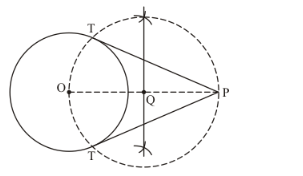
tep of construction

Step: I- First of all we draw a circle of radius.

Step: II- Make a point P at a distance of, and join  .

Step: III -Draw a right bisector of, intersecting  at Q .

Step: IV- Taking Q as centre and radius, draw a circle to intersect the given circle at T and T’.

Step: V- Joins PT and PT’ to obtain the require tangents.

Thus, are the required tangents.

Find the length of tangents.

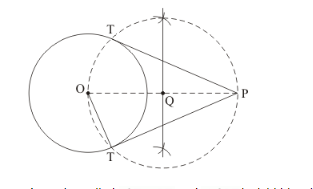
As we know that $O T \perp P T$ and $\triangle O P T$ is right triangle.

Therefore,

$O T=6 \mathrm{~cm}$ and $P O=10 \mathrm{~cm}$

In $\triangle O P T$,

$P T^{2}=O P^{2}-O T^{2}$

$=10^{2}-6^{2}$

$=100-36$

$=64$

$P T=\sqrt{64}$

$=8$

Thus, the length of tangents $=8 \mathrm{~cm}$