Due to the presence of the current

Question:

Due to the presence of the current $\mathrm{I}_{1}$ at the origin:-

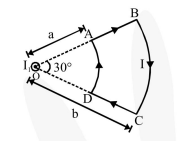
A current loop $\mathrm{ABCD}$ is held fixed on the plane of the paper as shown in the figure. The arcs $\mathrm{BC}$ (radius $=b$ ) and DA (radius $=a$ ) of the loop are joined by two straight wires AB and CD. A steady current $\mathrm{I}$ is flowing in the loop. Angle made by $\mathrm{AB}$ and $\mathrm{CD}$ at the origin $\mathrm{O}$ is $30^{\circ}$. Another straight thin wire with steady current $I_{1}$ flowing out of the plane of the paper is kept at the origin.

  1. The magnitude of the net force on the loop is given by $\frac{I_{1} I}{4 \pi} \mu_{0}\left[2(b-a)+\frac{\pi}{3}(a+b)\right]$

  2. The magnitude of the net force on the loop is given by $\frac{\mu_{0} I I_{1}}{24 a b}(b-a)$

  3. The forces on $\mathrm{AB}$ and $\mathrm{DC}$ are zero

  4. The forces on $\mathrm{AD}$ and $\mathrm{BC}$ are zero

Correct Option: , 2, 4

Solution:

For $\mathrm{AD}$ and $\mathrm{BC}, \overrightarrow{\mathrm{B}} \| \overrightarrow{\mathrm{dL}}$. Hence force on $\mathrm{AD}$ and $\mathrm{BC}$ is zero.

Leave a comment

None

All Study Material

Free Study Material