Each of the equal sides of an isosceles triangle is 25 cm.

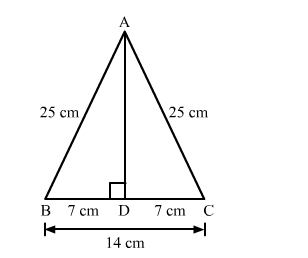
We know that the altitude drawn from the vertex opposite to the non equal side bisects the non equal side.
Suppose ABC is an isosceles triangle having equal sides AB and BC.
So, the altitude drawn from the vertex will bisect the opposite side.
Now, In right triangle ABD
By using Pythagoras theorem, we have

$\mathrm{AB}^{2}=\mathrm{BD}^{2}+\mathrm{DA}^{2}$

$\Rightarrow 25^{2}=7^{2}+\mathrm{DA}^{2}$

$\Rightarrow \mathrm{DA}^{2}=625-49$

$\Rightarrow \mathrm{DA}^{2}=576$

$\Rightarrow \mathrm{DA}=24 \mathrm{~cm}$