Question:
$\int \frac{x^{2}-2}{x^{5}-x} d x$
Solution:
By partial fractions,
$=\frac{x^{2}-2}{x^{2}-5}=\frac{x^{2}-2}{(x-1) x(x+1)\left(x^{2}+1\right)}=\frac{A}{x-1}+\frac{B}{x}+\frac{C}{x+1}+\frac{D}{x^{2}+1}$
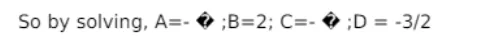
$=\int-\frac{d x}{4(x-1)}+\int \frac{2}{x} d x-\frac{1}{4} \int \frac{d x}{x+1}-\frac{3}{2} \int \frac{x d x}{x^{2}+1}$
$=-\frac{1}{4} \log (x-1)+2 \log x-\frac{1}{4} \log (x+1)-\frac{3}{4} \log \left(x^{2}+1\right)+c$
