Evaluate the following integrals:

Solution:

$\int \frac{e^{x}-1}{e^{x}+1} d x$

We can write above integrand as:

$\int\left(\frac{e^{x}}{e^{x}+1}-\frac{1}{e^{x}+1}\right) d x$

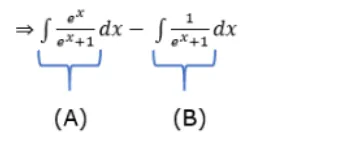
Considering integrand (A)

$A=\int \frac{e^{x}}{e^{x}+1} d x$

Put $e^{x}+1=t$

Differentiating w.r.t $x$ we get,

$e^{x} d x=d t$

Substituting values we get

$A=\int \frac{e^{x}}{e^{x}+1} d x=\int \frac{d t}{t} d x=\ln |t|+C$

Substituting the value of t we get,

$A=\ln \left|e^{x}+1\right|+C$

$\therefore A=\int \frac{e^{x}}{e^{x}+1} d x=\ln \left|e^{x}+1\right|+C \cdots(\mathrm{i})$

Considering integrand (B)

$B=\int \frac{1}{e^{x}+1} d x$

We can write above integral as

$\Rightarrow \int \frac{1+e^{x}-e^{x}}{e^{x}+1} d x$

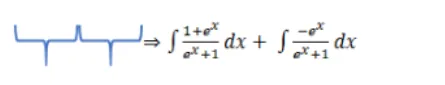
(1) (2)

Considering first integral:

$\int \frac{1+e^{x}}{1+e^{x}} d x$

Since the numerator and denominator are exactly same, our integrand simplifies to 1 and integrand becomes:

$\Rightarrow \int \mathrm{dx}$

$\Rightarrow \mathrm{x}$

$\therefore \int \frac{1+e^{x}}{1+e^{x}} d x=x$

Let $u=1+e^{x}, d u=e^{x} d x$

Apply u - substitution:

$\int \frac{1}{\mathrm{u}}(-\mathrm{du})=-\ln |u|$

Replacing the value of u we get,

$\int \frac{-e^{x}}{\sigma^{x}+1} d x=-\ln \left|1+e^{x}\right|+C \cdots(4)$

From (3) and (4) we get,

$\Rightarrow \int \frac{1+e^{x}}{e^{x}+1} d x+\int \frac{-e^{x}}{e^{x}+1} d x=x-\ln \left|1+e^{x}\right|+C$

$\therefore \mathrm{B}=\int \frac{1}{e^{x}+1} d x=x-\ln \left|1+e^{x}\right|+C-(\mathrm{ii})$

From (i) and (ii) we get,

$\int \frac{e^{x}}{e^{x}+1} d x-\int \frac{1}{e^{x}+1} d x=\left(\ln \left|e^{x}+1\right|-\left(x-\ln \left|1+e^{x}\right|\right)\right)+C$

$=2 \ln \left|e^{x}+1\right|-x+C$

$\therefore \int \frac{e^{x}-1}{e^{x}+1} d x=2 \ln \left|e^{x}+1\right|-x+C$