Evaluate the following limits:

To Find: Limits

NOTE: First Check the form of imit. Used this method if the limit is satisfying any one from 7 indeterminate form.

In this Case, indeterminate Form is $\frac{0}{0}$

By using L hospital Rule,

Differtiate both sides w.r.t $x$

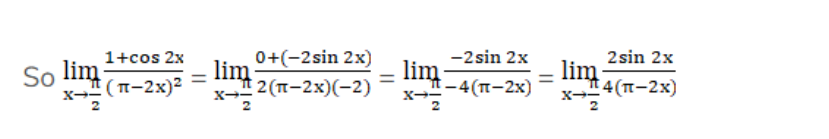
Again, indeterminate Form is $\frac{0}{0}$

So, Differtiate both sides w.r.t $x$ again, we have

$\lim _{x \rightarrow \frac{\pi}{2}} \frac{1+\cos 2 x}{(\pi-2 x)^{2}}=\lim _{x \rightarrow \frac{\pi}{2}} \frac{4 \cos 2 x}{4(-2)}=\lim _{x \rightarrow \frac{\pi}{2}} \frac{\cos 2 x}{(-2)}=\frac{\cos \pi}{(-2)}=\frac{-1}{(-2)}=\frac{1}{2}$

Therefore, $\lim _{x \rightarrow \frac{\pi}{2}} \frac{1+\cos 2 x}{(\pi-2 x)^{2}}=\frac{1}{2}$