Express each of the following in the form (a + ib)

Given: $\frac{(3-2 i)(2+3 i)}{(1+2 i)(2-i)}$

Firstly, we solve the given equation

$=\frac{3(2)+3(3 i)-2 i(2)+(-2 i)(3 i)}{(1)(2)+1(-i)+2 i(2)+2 i(-i)}$

$=\frac{6+9 i-4 i-6 i^{2}}{2-i+4 i-2 i^{2}}$

$=\frac{6+5 i-6(-1)}{2+3 i-2(-1)}$

$=\frac{6+6+5 i}{2+3 i+2}$

$=\frac{12+5 i}{4+3 i}$

Now, we rationalize the above by multiplying and divide by the conjugate of 4 + 3i

$=\frac{12+5 i}{4+3 i} \times \frac{4-3 i}{4-3 i}$

$=\frac{(12+5 i)(4-3 i)}{(4+3 i)(4-3 i)} \ldots$ (i)

Now, we know that,

$(a+b)(a-b)=\left(a^{2}-b^{2}\right)$

So, eq. (i) become

$=\frac{(12+5 i)(4-3 i)}{(4)^{2}-(3 i)^{2}}$

$=\frac{12(4)+12(-3 i)+5 i(4)+5 i(-3 i)}{16-9 i^{2}}$

$=\frac{48-36 i+20 i-15 i^{2}}{19-9(-1)}\left[\because i^{2}=-1\right]$

$=\frac{48-16 i-15(-1)}{16+9}\left[\because i^{2}=-1\right]$

$=\frac{48-16 i+15}{25}$

$=\frac{63-16 i}{25}$

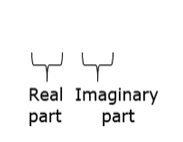
$=\frac{63}{25}-\frac{16}{25} i$