Find all the zeros of

Let $f(x)=x^{4}+x^{3}-23 x^{2}-3 x+60$

Since $\sqrt{3}$ and $-\sqrt{3}$ are the zeroes of $f(x)$, it follows that each one of $(x-\sqrt{3})$ and $(x+\sqrt{3})$ is a factor of $f(x)$.

Consequently, $(x-\sqrt{3})(x+\sqrt{3})=\left(x^{2}-3\right)$ is a factor of $f(x)$.

On dividing $f(x)$ by $\left(x^{2}-3\right)$, we get:

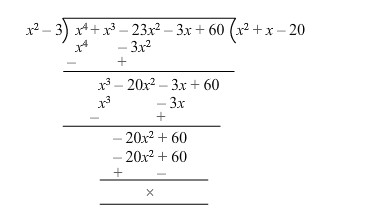
$\therefore f(x)=0$

$=>\left(x^{2}+x-20\right)\left(x^{2}-3\right)=0$

$=>\left(x^{2}+5 x-4 x-20\right)\left(x^{2}-3\right)$

$=>[x(x+5)-4(x+5)]\left(x^{2}-3\right)$

$=>(x-4)(x+5)(x-\sqrt{3})(x+\sqrt{3})=0$

$=>x=4$ or $x=-5$ or $x=\sqrt{3}$ or $x=-\sqrt{3}$

Hence, all the zeroes are $\sqrt{3},-\sqrt{3}, 4$ and $-5$.