Find the angle of elevation of the sum (sun's altitude) when the length of

Let be the angle of elevation of sun. Let be the vertical pole of height and  be the shadow of equal length.

Here we have to find angle of elevation of sun.

We have the corresponding figure as follows

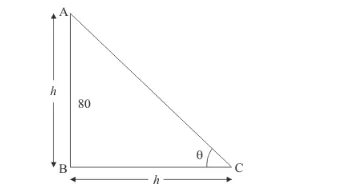
So we use trigonometric ratios to find the required angle.

In a triangle,

$\Rightarrow \quad \tan \theta=\frac{A B}{B C}$

$\Rightarrow \quad \tan \theta=\frac{h}{h}$

$\Rightarrow \quad \tan \theta=1$

$\Rightarrow \quad \theta=45^{\circ}$

Hence the angle of elevation of sun is $45^{\circ}$.