Find the area enclosed between two concentric circles of radii 3.5 cm and 7 cm.

We know the length of OA and OB.

$O A=r_{1}=3.5 \mathrm{~cm}$

$O B=r_{2}=7 \mathrm{~cm}$

Now we will calculate the area between the circles of radii 3.5 cm and 7 cm as shown below,

Area $=\pi r_{2}{ }^{2}-\pi r_{1}{ }^{2}$

$\therefore$ Area $=\pi\left(r_{2}^{2}-r_{1}^{2}\right)$

Substituting the values of $r_{1}, r_{2}$ and $\pi=\frac{22}{7}$ we get,

$\therefore$ Area $=\frac{22}{7} \times\left(7^{2}-3.5^{2}\right)$

$\therefore$ Area $=\frac{22}{7} \times(49-12.25)$

$\therefore$ Area $=\frac{22}{7} \times 36.75$

$\therefore$ Area $=22 \times 5.25$

$\therefore$ Area $=115.5$

Therefore, area enclosed by the two circles with radii $3.5 \mathrm{~cm}$ and $7 \mathrm{~cm}$ is $115.5 \mathrm{~cm}^{2}$.

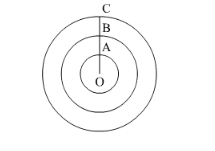
Now we will draw another circle such that radius of the circle will.

Now we will find $r_{3}$.

We have given that area enclosed by the circle with radius $r_{3}$ and $r_{2}$ is equal to the area of the enclosed by the circle with radius $r_{1}$ and $r_{2}$.

$\therefore \pi\left(r_{3}^{2}-r_{2}^{2}\right)=\pi\left(r_{2}^{2}-r_{1}^{2}\right)$

$\therefore\left(r_{3}^{2}-r_{2}^{2}\right)=\left(r_{2}^{2}-r_{1}^{2}\right)$

Substituting the values we get,

$\therefore\left(r_{3}^{2}-7^{2}\right)=\left(7^{2}-3.5^{2}\right)$

$\therefore\left(r_{3}^{2}-49\right)=(49-12.25)$

Adding 49 both sides of the equation we get,

$\therefore r_{3}^{2}=49-12.25+49$

$\therefore r_{3}^{2}=98-12.25$

$\therefore r_{3}^{2}=85.75$

Now we will take the square root.

$\therefore r_{3}=9.26$

Therefore, radius of the third circle is $9.26 \mathrm{~cm}$.