Find the area of a parallelogram ABCD in which AB = 14 cm,

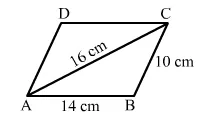
Let:

$a=10 \mathrm{~cm}, b=16 \mathrm{~cm}$ and $c=14 \mathrm{~cm}$

$s=\frac{a+b+c}{2}=\frac{10+16+14}{2}=20 \mathrm{~cm}$

By Heron's formula, we have :

Area of triangle $A B C=\sqrt{s(s-a)(s-b)(s-c)}$

$=\sqrt{20(20-10)(20-16)(20-14)}$

$=\sqrt{20 \times 10 \times 4 \times 6}$

$=\sqrt{10 \times 2 \times 10 \times 2 \times 2 \times 3 \times 2}$

$=10 \times 2 \times 2 \sqrt{3}$

$=69.2 \mathrm{~cm}^{2}$

We know that a diagonal divides a parallelogram into two triangles of equal areas.

$\therefore$ Area of parallelogram $A B C D=2($ Area of triangle $A B C)=2 \times 69.2 \mathrm{~cm}^{2}=138.4 \mathrm{~cm}^{2}$