Question:
Find the area of a parallelogram ABCD in which AB = 28 cm, BC = 26 cm and diagonal AC = 30 cm.
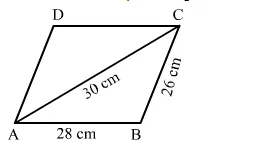
Solution:
Let:
$a=26 \mathrm{~cm}, b=30 \mathrm{~cm}$ and $c=28 \mathrm{~cm}$
$s=\frac{a+b+c}{2}=\frac{26+30+28}{2}=42 \mathrm{~cm}$
By Heron's formula, we have :
Area of triangle $A B C=\sqrt{s(s-a)(s-b)(s-c)}$
$=\sqrt{42(42-26)(42-30)(42-28)}$
$=\sqrt{42 \times 16 \times 12 \times 14}$
$=\sqrt{14 \times 3 \times 4 \times 4 \times 2 \times 2 \times 3 \times 14}$
$=14 \times 4 \times 2 \times 3$
$=336 \mathrm{~cm}^{2}$
We know that a diagonal divides a parallelogram into two triangles of equal areas.
$\therefore$ Area of parallelogram $A B C D=2$ (Area of triangle $A B C$ ) $=2 \times 336=672 \mathrm{~cm}^{2}$
