Find the area of the following figure,

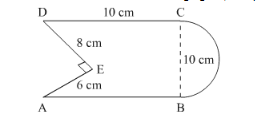
Let the area of square ABCD be A.

It s given that, $\mathrm{AB}=10 \mathrm{~cm}$

So, $A=10 \times 10 \mathrm{~cm}^{2}$

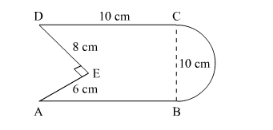
It is given that a semicircle is attached to one side of the square.

The diameter of semicircle $=10 \mathrm{~cm}$

So, radius $r$ of semicircle $=5 \mathrm{~cm}$

We know that the area of semicircle of radius r is

$A^{\prime}=\frac{1}{2} \times \frac{22}{7} \times 5 \times 5$

Substituting the value of r,

$A^{\prime}=\frac{1}{2} \times \frac{22}{7} \times 5 \times 5$

$=39.3 \mathrm{~cm}^{2}$

From the above figure it is seen that a right angle triangle is cutoff from one side of square.

The area of right angle triangle $=\frac{1}{2} b h$

$=\frac{1}{2} \times 8 \times 6$

$=24 \mathrm{~cm}^{2}$

Now, the area $A^{*}$ of above figure is,

$A^{n}=$ Area of square $+$ Area of semicircle-Area of triangle

$=100+39.3-24$

$=115.3 \mathrm{~cm}^{2}$

Hence area of given figure is $115.3 \mathrm{~cm}^{2}$