Find the area of the quadrilateral ABCD in which BCD is an equilateral triangle, each of whose sides is 26 cm,

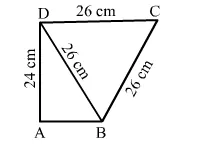
We know that $\triangle B A D$ is a right-angled triangle.

$\therefore A B=\sqrt{B D^{2}-A D^{2}}=\sqrt{26^{2}-24^{2}}=\sqrt{676-576}=\sqrt{100}=10 \mathrm{~cm}$

Now,

Area of triangle $B A D=\frac{1}{2} \times$ Base $\times$ Height

$=\frac{1}{2} \times A B \times A D$

$=\frac{1}{2} \times 10 \times 24$

$=120 \mathrm{~cm}^{2}$

Also, we know that $\triangle B D C$ is an equilateral triangle.

$\therefore$ Area of equilateral triangle $=\frac{\sqrt{3}}{4} \times(\text { Side })^{2}$

$=\frac{\sqrt{3}}{4} \times(26)^{2}$

$=\frac{\sqrt{3}}{4} \times 676$

$=169 \sqrt{3}$

$=292.37 \mathrm{~cm}^{2}$

Now,

Area of quadrilateral $A B C D=$ Area of $\triangle A B D+$ Area of $\triangle B D C$

$=(120+292.37) \mathrm{cm}^{2}=412.37 \mathrm{~cm}^{2}$

Perimeter of ABCD = AB + BC + CD + DA = 10 + 26+ 26 + 24 = 86 cm