Find the equation of the plane which is perpendicular to the plane 5x + 3y + 6z + 8 = 0

The given planes are

P1: 5x + 3y + 6z + 8 = 0

P2: x + 2y + 3z – 4 = 0

P3: 2x + y – z + 5 = 0

Now, the equation of the plane passing through the line of intersection of P1 and P3 is

(x + 2y + 3z – 4) + λ(2x + y – z + 5) = 0

(1 + 2λ)x + (2 + λ)y + (3 – λ)z – 4 + 5λ = 0 …. (i)

From the question its understood that plane (i) is perpendicular to P1, then

5(1 + 2λ) + 3(2 + λ) + 6(3 – λ) = 0

5 + 10λ + 6 + 3λ + 18 – 6λ = 0

7λ + 29 = 0

λ = -29/7

Putting the value of ; in equation (i), we get

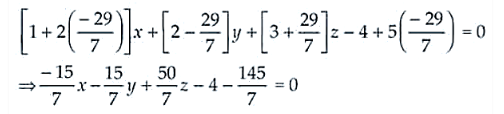
-15x – 15y + 50z – 28 – 145 = 0

-15x – 15y + 50z – 173 = 0 ⇒ 51x + 15y – 50z + 173 = 0

Thus, the required equation of plane is 51x + 15y – 50z + 173 = 0.