Find the image of the point (3, 8)

The equation of the given line is

x + 3y = 7 … (1)

Let point B (a, b) be the image of point A (3, 8).

Accordingly, line (1) is the perpendicular bisector of AB.

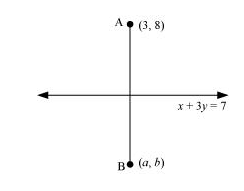
Slope of $\mathrm{AB}=\frac{b-8}{a-3}$, while the slope of line $(1)=-\frac{1}{3}$

Since line (1) is perpendicular to AB,

$\left(\frac{b-8}{a-3}\right) \times\left(-\frac{1}{3}\right)=-1$

$\Rightarrow \frac{b-8}{3 a-9}=1$

$\Rightarrow b-8=3 a-9$

$\Rightarrow 3 a-b=1$ $\ldots(2)$

Mid-point of $\mathrm{AB}=\left(\frac{a+3}{2}, \frac{b+8}{2}\right)$

The mid-point of line segment AB will also satisfy line (1).

Hence, from equation (1), we have

$\left(\frac{a+3}{2}\right)+3\left(\frac{b+8}{2}\right)=7$

$\Rightarrow a+3+3 b+24=14$

$\Rightarrow a+3 b=-13$ $\ldots(3)$

On solving equations (2) and (3), we obtain a = –1 and b = –4.

Thus, the image of the given point with respect to the given line is (–1, –4).