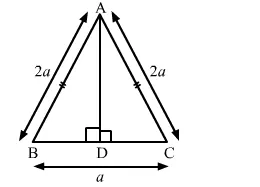
Find the length of altitude AD of an isosceles ∆ABC in which

In isosceles ∆ ABC, we have:
AB = AC = 2a units and BC = a units
Let AD be the altitude drawn from A that meets BC at D.
Then, D is the midpoint of BC.

$\mathrm{BD}=\mathrm{BC}=\frac{a}{2}$ units

Applying Pythagoras theorem in right-angled ∆ABD, we have:

$A B^{2}=A D^{2}+B D^{2}$

$A D^{2}=A B^{2}-B D^{2}=(2 a)^{2}-\left(\frac{a}{2}\right)^{2}$

$A D^{2}=4 a^{2}-\frac{a^{2}}{4}=\frac{15 a^{2}}{4}$

$A D=\sqrt{\frac{15 a^{2}}{4}}=\frac{a \sqrt{15}}{2}$ units