Question:
Find the mean deviation about the mean of the distribution:
Solution:
Given data distribution
Now we have to find the mean deviation about the mean of the distribution Construct a table of the given data
We know that mean,
$\overline{\mathrm{X}}=\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}=\frac{433}{20}=21.65$
To find mean deviation we have to construct another table
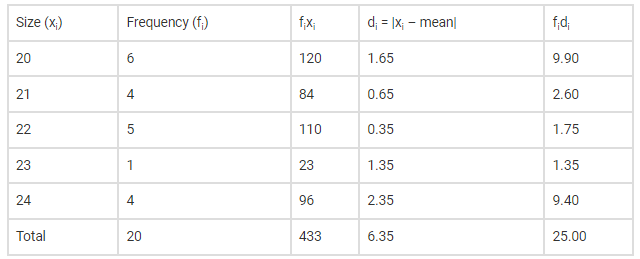
Hence Mean Deviation becomes,
M. $\mathrm{D}=\frac{\sum \mathrm{f}_{\mathrm{i}} \mathrm{d}_{\mathrm{i}}}{\sum \mathrm{f}_{\mathrm{i}}}=\frac{25}{20}=1.25$
Therefore, the mean deviation about the mean of the distribution is 1.25