Find the mean deviation about the median for the following data :

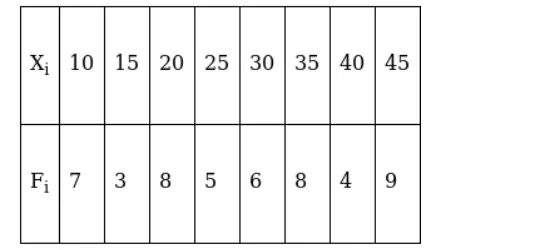
The given observations are in ascending order. Adding a row corresponding to cumulative frequencies to the given data, we get,

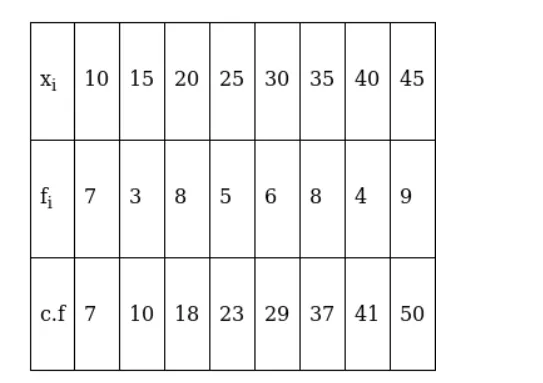
Now, $N=50$ which is even.

Median is the mean of the $25^{\text {th }}$ observation and $26^{\text {th }}$ observation. Both of these observations lie in the cumulative frequency 29 , for which the corresponding observation is 30 .

Median $(M)=\frac{25^{\text {th }} \text { observation }+26^{\text {th }} \text { observation }}{2}=\frac{30+30}{2}=30$

Now, absolute values of the deviations from the median,

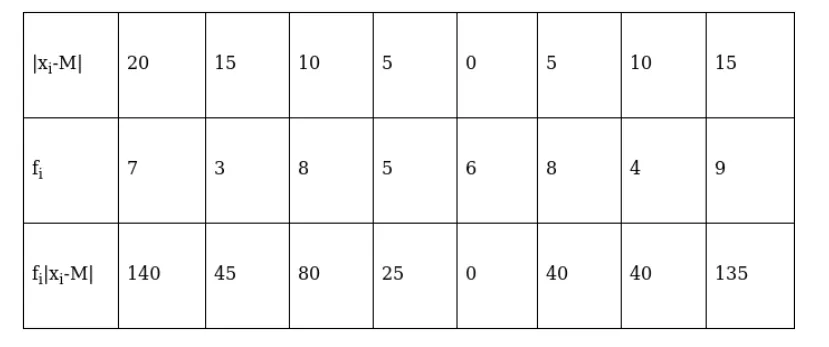
We have, $\sum_{\mathrm{i}=1}^{5} \mathrm{f}_{\mathrm{i}}=50$ and $\sum_{\mathrm{i}=1}^{5} \mathrm{f}_{\mathrm{i}}\left|\mathrm{x}_{\mathrm{i}}-\mathrm{M}\right|=505$

$\therefore \mathrm{M} . \mathrm{D}(\mathrm{M})=\frac{\sum_{\mathrm{i}=1}^{5} \mathrm{f}_{\mathrm{i}}\left|\mathrm{x}_{\mathrm{i}}-\mathrm{M}\right|}{\sum_{\mathrm{i}=1}^{5} \mathrm{f}_{\mathrm{i}}}$

$=\frac{505}{50}=10.1$