Find the mean deviation about the median for the following data :

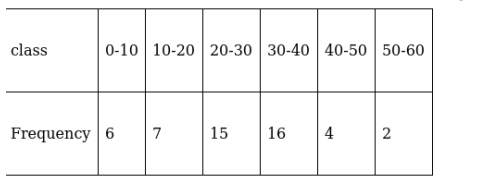
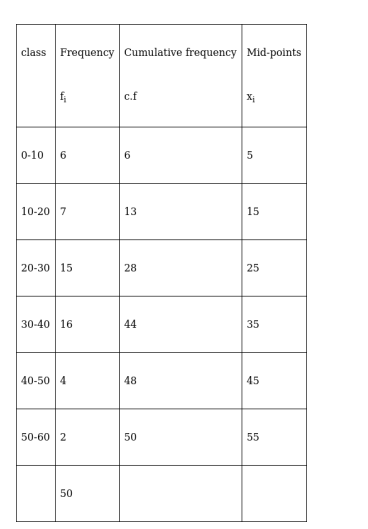
The class interval containing $\frac{\mathrm{N}^{\mathrm{th}}}{2}$ or 25th item is 20-30. Therefore, 20–30 is the median class. We know that

Median $=1+\frac{\frac{\mathrm{N}}{2}-\mathrm{C}}{\mathrm{f}} \times \mathrm{h}$

Here, $I=20, C=13, f=15, h=10$ and $N=50$

Therefore, $\quad$ Median $=20+\frac{\frac{50}{2}-13}{15} \times 10=20+8=28$

Now,

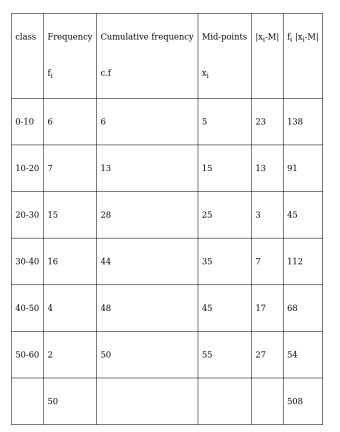
We have, $\sum_{\mathrm{i}=1}^{6} \mathrm{f}_{\mathrm{i}}=50_{\text {and }} \sum_{\mathrm{i}=1}^{6} \mathrm{f}_{\mathrm{i}}\left|\mathrm{x}_{\mathrm{i}}-\mathrm{M}\right|=508$

$\therefore \mathrm{M} . \mathrm{D}(\mathrm{M})=\frac{\sum_{\mathrm{i}=1}^{6} \mathrm{f}_{\mathrm{i}}\left|\mathrm{x}_{\mathrm{i}}-\mathrm{M}\right|}{\sum_{\mathrm{i}=1}^{6} \mathrm{f}_{\mathrm{i}}}$

$=\frac{508}{50}=10.16$