Find the mean deviation about the median for the following data :

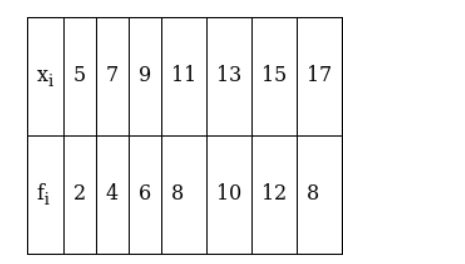
The given observations are in ascending order. Adding a row corresponding to cumulative frequencies to the given data, we get,

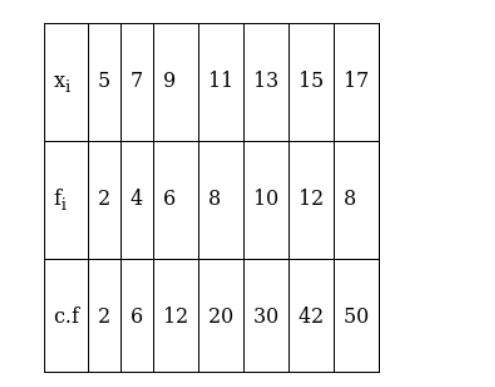
Now, $\mathrm{N}=50$ which is even.

Median is the mean of the $25^{\text {th }}$ observation and $26^{\text {th }}$ observation. Both of these observations lie in the cumulative frequency 30 , for which the corresponding observation is 13 .

Median $(M)=\frac{25^{\text {th }} \text { observation }+26^{\text {th }} \text { observation }}{2}=\frac{13+13}{2}=13$

Now, absolute values of the deviations from the median,

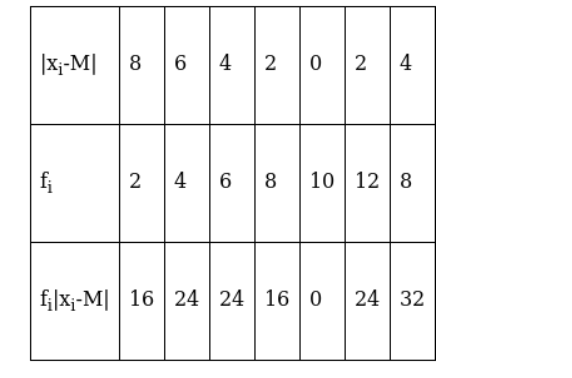
We have, $\sum_{\mathrm{i}=1}^{5} \mathrm{f}_{\mathrm{i}}=50$ and $\sum_{\mathrm{i}=1}^{5} \mathrm{f}_{\mathrm{i}}\left|\mathrm{x}_{\mathrm{i}}-\mathrm{M}\right|=136$

$\therefore M . D(M)=\frac{\sum_{i=1}^{5} f_{i}\left|x_{i}-M\right|}{\sum_{i=1}^{5} f_{i}}$

$=\frac{136}{50}=2.72$