Find the perimeter and area of the quadrilateral ABCD in which AB = 21 cm,

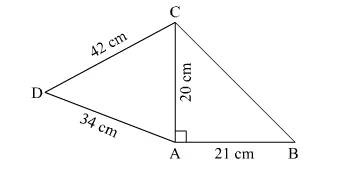
In right angled ∆ABC,

$B C^{2}=A B^{2}+A C^{2}$         (Pythagoras Theorem)

$\Rightarrow B C^{2}=21^{2}+20^{2}$

$\Rightarrow B C^{2}=441+400$

$\Rightarrow B C^{2}=841$

⇒ BC = 29 cm

Area of $\triangle A B C=\frac{1}{2} \times A B \times A C$

$=\frac{1}{2} \times 21 \times 20$

$=210 \mathrm{~cm}^{2}$        ....(1)

$\ln \Delta A C D$

The sides of the triangle are of length 20 cm, 34 cm and 42 cm.
∴ Semi-perimeter of the triangle is

$s=\frac{20+34+42}{2}=\frac{96}{2}=48 \mathrm{~cm}$

∴ By Heron's formula,

Area of $\Delta A C D=\sqrt{s(s-a)(s-b)(s-c)}$

$=\sqrt{48(48-20)(48-34)(48-42)}$

$=\sqrt{48(28)(14)(6)}$

$=336 \mathrm{~cm}^{2}$         $\ldots(2)$

Thus,
Area of quadrilateral ABCD = Area of ∆ABC + Area of ∆ACD

$=(210+336) \mathrm{cm}^{2}$

$=546 \mathrm{~cm}^{2}$

Also,

Perimeter of quadrilateral ABCD = (34 + 42 + 29 + 21) cm
= 126 cm

Hence, the perimeter and area of quadrilateral $A B C D$ is $126 \mathrm{~cm}$ and $546 \mathrm{~cm}^{2}$, respectively.