Find the principal value of :

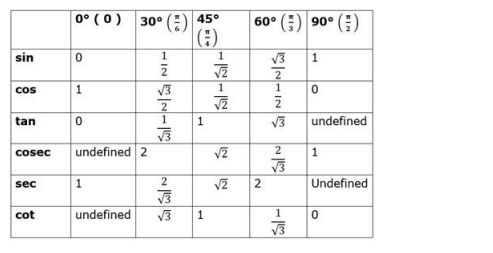
Trigonometric Table

(i) Let $\sin ^{-1}\left(\frac{\sqrt{3}}{2}\right)=\mathrm{x}$

$\Rightarrow \frac{\sqrt{3}}{2}=\sin x$ [ We know which value of $x$ when placed in sin gives us this answer]

$\therefore \mathrm{X}=\frac{\pi}{3}$

(ii) Let $\sin ^{-1}\left(\frac{1}{2}\right)=x$

$\Rightarrow \frac{1}{2}=\sin x$ [We know which value of $x$ when put in this expression will give us this result]

$\Rightarrow \mathrm{x}=\frac{\pi}{6}$

(iii) Let $\cos ^{-1}\left(\frac{1}{2}\right)=\mathrm{x}$

$\Rightarrow \frac{1}{2}=\cos x$ [We know which value of $x$ when put in this expression will give us this result]

$\therefore \mathrm{X}=\frac{\pi}{3}$

(iv) Let $\tan ^{-1}(1)=x$

$\Rightarrow 1=\tan x$ [We know which value of $x$ when put in this expression will give us this result]

$\therefore \mathrm{X}=\frac{\pi}{4}$

(v) Let $\tan ^{-1}\left(\frac{1}{\sqrt{3}}\right)=\mathrm{x}$

$\Rightarrow \frac{1}{\sqrt{3}}=\tan x$ [We know which value of $x$ when put in this expression will give us this result]

$\therefore \mathrm{X}=\frac{\pi}{6}$

(vi) Let $\sec ^{-1}\left(\frac{2}{\sqrt{3}}\right)=x$

$\Rightarrow \frac{2}{\sqrt{3}}=\sec x$ [We know which value of $x$ when put in this expression will give us this result]

$\therefore \mathrm{X}=\frac{\pi}{6}$

(vii) Let $\operatorname{cosec}^{-1}(\sqrt{2})=x$

$\Rightarrow \sqrt{2}=\operatorname{cosec} x$

[We know which value of x when put in this expression will give us this result]

$\therefore \mathrm{X}=\frac{\pi}{4}$