Question:
Find the value of p, when the mean of the following distribution is 20.
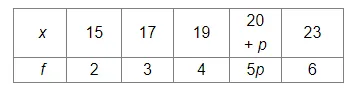
Solution:
We know that,
Mean $=\frac{\sum x_{i} f_{i}}{\sum f_{i}}$
For the following data:
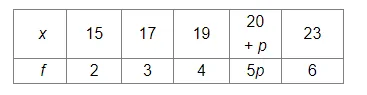
Mean $=\frac{(15 \times 2)+(17 \times 3)+(19 \times 4)+((20+p) \times 5 p)+(23 \times 6)}{2+3+4+5 p+6}$
$\Rightarrow 20=\frac{30+51+76+100 p+5 p^{2}+138}{15+5 p}$
$\Rightarrow 20(15+5 p)=5 p^{2}+100 p+295$
$\Rightarrow 300+100 p=5 p^{2}+100 p+295$
$\Rightarrow 5 p^{2}=300-295$
$\Rightarrow 5 p^{2}=5$
$\Rightarrow p^{2}=\frac{5}{5}$
$\Rightarrow p^{2}=1$
$\Rightarrow p=\pm 1$
Hence, the value of $p$ is $\pm 1$.
